In today’s digital landscape, data centers are witnessing an unprecedented surge in the volume of data and information. The exponential growth of online content has transformed the storage landscape, pushing organizations to confront a new challenge beyond mere data storage. Alongside the imperative of storage, organizations are grappling with the need to master efficient access to this vast expanse of Big Data.
Now, it’s the age of AI, and you’ll hear almost everyone talk about it around you. One of the core algorithms of AI is Vector Search.
Vector Search algorithms have emerged as indispensable tools to navigate the data-rich terrain, offering innovative solutions to institutions worldwide. With consistent developments in AI and Machine Learning, this science of Vector Search and Machine learning algorithms will only expand more. To keep you updated, we bring this article for you. This article explores the impact of vector search on the paradigm of web data access and some core principles.
What is Vector Search?
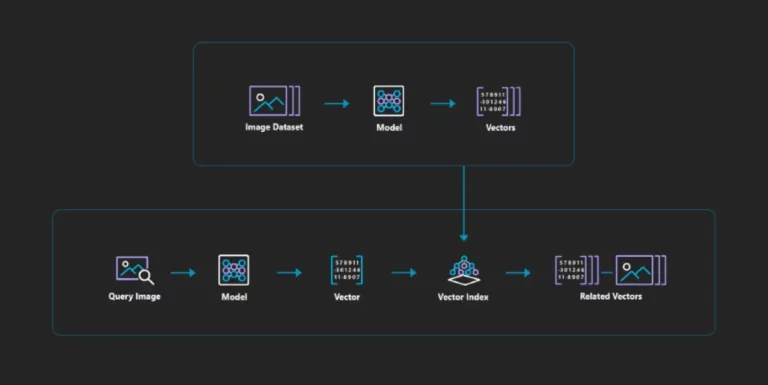
We are going to dive deeper into how vector search algorithms are a great help in enhancing the user experience for modern applications. Still, first, we need to look at what exactly is vector search, and even before that, let’s answer the question – What is a vector? Vector is a mathematical term representing data in a multi-dimensional space. These vectors represent various types of data, such as text, images, or any other structured or unstructured information. Vector Search is an algorithm that searches for information in a vector database by mapping each data item to a vector representation of itself. The key innovation behind vector search lies in these vectors capturing the raw data and the relationships and similarities between data items.
Vector Space Models?
A very obvious question when discussing vectors is how exactly are data items represented as vectors? “Vector Space Models” is the answer to this question. Vector Space Models are mathematical techniques that map data items to a vector representation where each dimension of the space corresponds to a unique term. These models work by identifying underlying relationships between words, documents, or any other textual elements within a multi-dimensional space.
Similarity Metrics
Vector Search involves finding similarities between data points represented as vectors in a high-dimensional space. With the advent of vector databases, this technique has gained prominence, where vast datasets can be efficiently organized and queried based on vector similarity. Vector search’s ability to handle complex data types like images, text, and audio has revolutionized information retrieval, recommendation systems, and even bioinformatics, underscoring its pivotal role in shaping modern data-driven solutions.
When it comes to vector similarity, various distance metrics are used to establish how similar two vectors are—calculating the distance metric between two data points to account for similarity or dissimilarity between the points. We have numerous approaches and methodologies, and based on these methods, we classify distance metrics into various types. Let’s look at some of the most prominent classifications of Distance Metrics.
Euclidean Distance
The Euclidean Distance between two data points lets us calculate the shortest distance between them. We compute the square root of the sum of squares of differences between corresponding elements to calculate the Euclidean Distance Metric between two data points.
Manhattan Distance
Manhattan is the difference which is always computed by subtracting the smaller value from the greater value. Manhattan Distance is also known as city block distance.
Minkowski Distance
Sometimes data scientists want to find a middle ground between using the Euclidean Distance Metric and the Manhattan Distance Metric. For these cases, we use the Minkowski Distance. Computing the Minkowski Distance Metric is really helpful when we need to find the optimal correlation or classification of vector database.
The Minkowski distance can also be viewed as a multiple of the power mean of the component-wise differences between V1 and V2, where V1 and V2 are both vector databases. Here’s the mathematical representation of the formula used to calculate the Minkowski Distance Metric.
Hamming Distance
The Hamming Distance between two strings of the same length is the number of positions at which the corresponding characters differ. The characters can be letters, bits, or decimal digits, among other possibilities.
Scalability of Vector Search
Vector Search gets to the heart of the issue. These algorithms are designed to handle large databases efficiently. How do they manage this? Through clever indexing and sorting methods, real-time information retrieval.
Furthermore, vector search supports parallel processing, allowing simultaneous operations on different pieces of data. This greatly enhances the efficiency of any application, as one process can run while others are initiated. In today’s data-driven world, where information volume grows exponentially, vector search is vital for organizations seeking seamless access to their Big Data, ensuring that the ever-expanding digital landscape remains navigable.
Scaling
Another benefit of using vector search algorithms is that vector search systems can scale vertically (adding more resources to a single server) and horizontally (adding more servers to a cluster) to meet growing demands.
Performance Optimization
Vector Search is particularly famous for having the ability to improve the performance of applications by applying optimization techniques. These optimization techniques involve indexing strategies, dimensionality reduction, sorting operations, caching, query optimization, load balancing, hardware acceleration, query vector compression, monitoring and profiling, rigorous testing, and resource management.
Limitations of Vector Search
Of course, Vector Search algorithms, too, like any other algorithm, have some limitations.
- High-Dimensional Space: Since the dimensional space used to map vectors is multi-dimensional, the data points become sparse, impacting the efficiency and accuracy of similarity calculations.
- Data Quality: Data quality wholly depends on the quality of the vector representations. If a correct Vector Space Model is not chosen to represent data points as vectors, the data retrieval quality will have to suffer.
- Lack of Historical Data: Recommender systems using vector search may struggle when dealing with new users or items because there is insufficient historical data to create meaningful vectors.